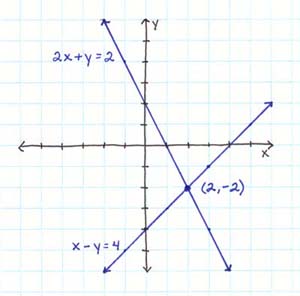
| Example 1: | Solve |
| x - y = 4 | |
| 2x + y = 2 |
When we change the equations to slope-intercept form...
x - y = 4 becomes y = x - 4
slope = 1
y-intercept = -42x + y = 2 becomes y = -2x + 2
slope = -2
y-intercept = 2When we graph this it appears like that below:

Since the two lines intersect, we look for the exact point where they cross and that becomes our solution. To check the solution we can plug it back into the original equations. If we get true statements, then the solution is correct. If we get false statements we need to check our work.
| x - y = 4 x = 2 and y = -2 (2) - (-2) = 4 4 = 4 True |
2x + y = 2 x = 2 and y = -2 2(2) + (-2) = 2 4 + (-2) = 2 2 = 2 True |